Les bobines à noyau de fer

Tout comme le circuit magnétique, la bobine à noyau de fer est constituée d’un fil conducteur enrouléautour d’un noyau en fer (ferromagnétique). Développons en premier lieu, ce qu’est une bobine parfaite.

Bobine idéale

Une bobine idéale est un circuit magnétique « idéal » c’est-à-dire sans flux de fuite.

Loi de Lenz-Faraday

Lorsqu’il y a variation de courant, il y a également variation de flux magnétique (force magnétomotrice), ce phénomène induit une force électromotrice d’induction électromagnétique traduit par la loi de Lens-Faraday :

La force électromotrice inductive e(t) ainsi créée est orientée :

• positivement, lorsque la tension orientée dans la même direction que le courant, ou
• négativement, lorsqu’elle génère des courants s’opposant à la variation du flux.

Convention électromagnétique – Règle des points

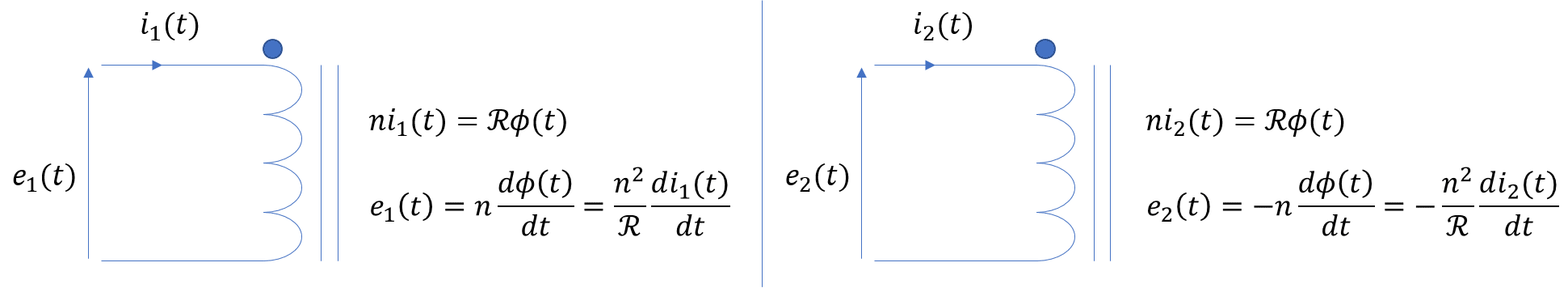
Bobine réelle

En outre, une bobine réelle est une bobine idéale pour laquelle il apparaît un flux de fuite.

Relation entre flux

Par conséquent, il existe un flux Φ_e dans l’enroulement qui somme le flux de fuite Φ_f avec que le flux principal Φ_p :

Tension aux bornes de la bobine

La tension u(t) aux bornes de la bobine et l’intensité i(t) du courant sont reliés par l’équation différentielle :

tel que r est la résistance des bobinages (dans le cas d’une bobine parfaite r = 0) et L_f l’inductance de fuite.

Modèle électrique de la bobine

Ensuite, le modèle le plus simple décrivant l’équation précédente est celui correspondant à l’association d’une bobine d’inductance et d’une résistance en série :

Circuit magnétique non-saturé

Dans le cas d’un circuit magnétique linéaire, la loi d’Hopkinson permet d’écrire :

Par conséquent, cette équation mène à ce schéma équivalent :

Circuit magnétique saturé

Contrairement aux circuits magnétiques non-saturés, les circuits magnétiques saturés ont des amplitudes en courants et tensions élevées. En conséquence, la saturation est vite atteinte engendrant un comportement non-linéaire (μ_r ≈ constante). De ce fait, ℜ et L ne peuvent plus être définies. L’équation devient donc :

Hypothèse de Kapp

L’hypothèse de Kapp consiste à négliger le flux de fuite et la résistance de bobinage, ce qui donne :

Remarque : Généralement u(t) est sinusoïdale et compte tenu de l’hypothèse précédente, Φ(t) est lui même sinusoïdale. On parle alors de fonctionnement à flux forcé.

Relation de Boucherot

De même, la relation de Boucherot permet d’établir le lien entre l’induction et la tension.

Les pertes

En outre, parlons des différentes pertes qu’il existe dans une bobine à noyau de fer. On différencie les pertes cuivre appelé aussi pertes Joules, des pertes fer. Les pertes cuivre se retrouvent dans les circuits électriques des bobinages, elles correspondent à la puissance dégagée par effet joule tandis que les pertes fer correspondent à la puissance dépensée dans les circuits magnétiques. Ainsi, les pertes fer se divisent en deux catégories, les pertes par hystérésis et par courant de Foucault.

Phénomène d’hystérésis magnétique

En raison de la présence d’un champ d’induction alternatif, les domaines de l’échantillon du métal se déplacent les uns par rapport aux autres. On appelle ce phénomène, le cycle d’hystérésis. Lors de chaque cycle d’hystérésis, il y a frottement des différents domaines magnétiques, ce qui provoque une perte d’énergie se traduisant par une augmentation de la température dans le fer. Ainsi, les pertes par hystérèse sont liées à la surface du cycle. Voici un exemple de cycle d’hystérésis lorsqu’on magnétise un morceau de matériau ferromagnétique doux jusqu’à saturation et que l’on diminue l’excitation H :

On note H_c le champ coercitif et B_r le champ rémanent (« rester »).

Remarque : Le trigger que l’on a tous utilisé au moins une fois réalise une hystérésis.

Formule pour les pertes par hystérésis magnétique

où k₁ et α sont caractéristiques du matériau, f la fréquence du cycle et B la valeur du champ magnétique.

Courant de Foucault

Dans la plupart des cas, le matériau utilisé pour générer les lignes de champ est conducteur, ainsi il y avariation du champ magnétique B et donc apparition de courants induits engendrant des pertes par effet joule. Afin de palier ces pertes, il existe deux solutions :

• Diminuer l’épaisseur du matériau magnétique (circuits magnétiques feuilleté : tôles isolées entre elles)
• Utiliser des matériaux magnétiques à résistivité plus élevée comme la tôle d’acier au silicium ou ferrites à fréquence élevée)

Formule pour les pertes par courant de Foucault

où k₂ est caractéristique du matériau, f la fréquence du cycle et B la valeur du champ magnétique.

Modèle électrique d’une bobine à noyau de fer

Enfin, voici le modèle électrique d’une bobine à noyau de fer :

Source : Cours électrotechnique 1 Licence PCI, Nicolas Naudé (Institut National Universitaire Champollion)/Lionel Laudebat (Université Paul Sabatier)–  Maîtres de conférences et chercheurs (LAPLACE)