.
Introduction
.
Comme nous le verrons dans l’article sur les convertisseurs, ce dernier convertit le signal échantillonné en signal quantifié et codé sous forme de valeurs qui définissent l‘état des variables :
- 0 ou 1
- Vrai ou Faux
- État Haut ou état Bas
Ainsi, la combinaison de l’état de ces variables d’entrées définit la fonction logique.
.
Fonctions logiques
.
Il existe deux sortes de fonctions logiques, les fonctions logiques simples et composées. De même, celles-ci peuvent être représentés sous forme d’équation logique, de table de vérité, de chronogramme ou encore de schéma de contact électrique.
.
Fonctions logiques simples
Pour bien comprendre ce qu’il se passe, nous allons illustrer les trois fonctions logiques (ET, OU et NON) à l’aide de circuits électriques (composés d’une ampoule en sortie afin de voir s’il y a une tension en sortie associés à la représentation temporelle des tensions aux bornes des interrupteurs et de l’ampoule), de leur table de vérité ainsi que leur équation logique.
.
ET (AND)
.
Grâce à ce schéma, on en déduit ainsi la table de vérité :
.
En conclusion, la fonction logique a pour équation logique :
.
OU (OR)
.
Grâce à ce schéma, on en déduit ainsi la table de vérité :
.
En conclusion, la fonction logique a pour équation logique :
.
NON (NOT)
.
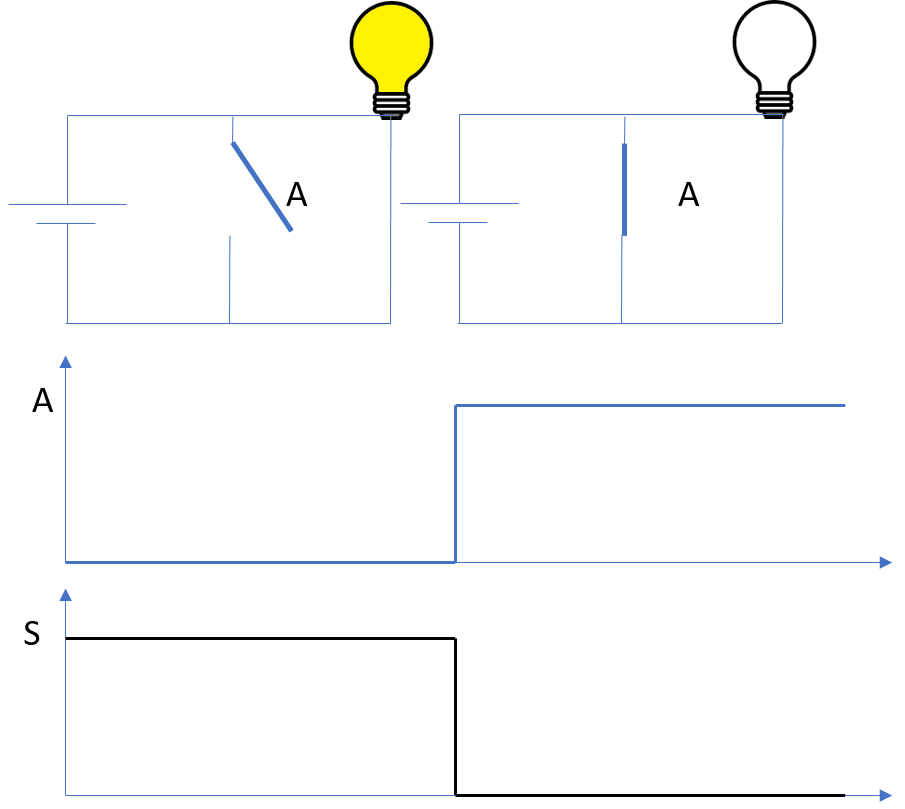
Grâce à ce schéma, on en déduit ainsi la table de vérité :
.
En conclusion, la fonction logique a pour équation logique :
.
Fonctions logiques composées
Également, pour bien comprendre ce qu’il se passe, nous allons illustrer les trois fonctions logiques composées (NON-ET, NON-OU et OU exclusif) à l’aide des symboles des fonctions logiques simples, de leur table de vérité ainsi que leur équation logique.
.
NON-ET (NAND)
La fonction NON-ET (NAND) est composée comme son nom l’indique des fonctions ET (AND) et NON (NOT) :
.
Grâce à ce schéma, on en déduit ainsi la table de vérité :
.
En conclusion, la fonction logique a pour équation logique :
.
NON-OU (NOR)
La fonction NON-OU (NOR) est composée comme son nom l’indique des fonctions OU (OR) et NON (NOT) :
.
Grâce à ce schéma, on en déduit ainsi la table de vérité :
.
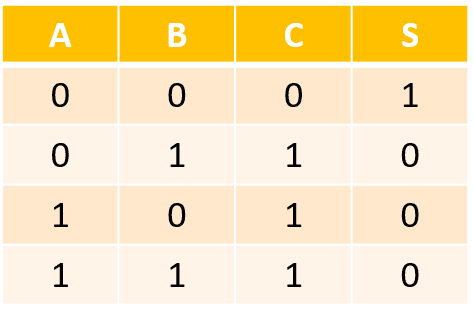
En conclusion, la fonction logique a pour équation logique :
.
Ou exclusif (XOR)
La fonction OU exclusif (XOR) est composée des trois fonctions OU (OR), NON-ET (NAND) et ET (AND) :
.
Grâce à ce schéma, on en déduit ainsi la table de vérité :
.
En conclusion, la fonction logique a pour équation logique :
Merci !
Peut servir pour la SI en term 😉
Merci 🙂
Avec plaisir Youssef et Rwanito 😉