Introduction:
Avant de commencer cet article, il est nécessaire de savoir que l’on utilise le modèle de connaissance afin de passer du système physique à sa représentation mathématique pour déterminer la fonction de transfert de ce système, cela revient à utiliser les lois de la physique adéquats.
Que l’on parle de circuit RLC , phénomène physique… tous les systèmes dynamiques peuvent être décrit par des équations différentielles composés d’une entrée et d’une sortie
.

Dans le cas général (ordre ) d’un système linéaire linéaire invariant dans le temps :
Deux solutions s’offrent donc à nous pour résoudre cette équation différentielle d’ordre ,
- résolution temporelle ( = résolution d’équations différentielles)
Premièrement, résoudre temporellement l’équation différentielle c’est obtenir pour une entrée donnée, la réponse temporelle
correspondante. Mais l’inconvénient de cette solution est que l’outil mathématique utilisé est rapidement complexe à manipuler. Il est donc nécessaire de se pencher vers une autre solution.
- La résolution symbolique pour déterminer la fonction de transfert
Enfin, on introduit l’opérateur (variable de Laplace) qui permettra de transformer toutes les équations différentielles en polynômes en
. La transformée de Laplace est un outil puissant adapté à l’analyse de certains problèmes de l’électronique, l’automatique… Ainsi, à chaque fois que l’on dérive par rapport au temps dans une équation différentielle revient à multiplier par l’opérateur
dans un polynôme, lorsque les conditions initiales sont nulles on a :
La fonction de transfert traduit l’entrée
(
) sur la sortie
(
) :

Dans notre cas général,
Réponse fréquentielle (Harmonique) d’un système (a partir de la fonction de transfert)
Pour faire une analyse harmonique d’un système en régime établi (permanent), on peut faire une représentation graphique appelée réponse fréquentielle « facilement » réalisable à partir de la fonction de transfert.
Pour cela, il y a 5 étapes à suivre :
- Obtenir la fonction de transfert
- Poser
dans
pour calculer
- Calculer le module
et le traduire en dB
- Calculer l’argument
- Faire le calcul du module et de l’argument aux limites
et
et si nécessaire pour des points remarquables.
Ensuite, la réponse fréquentielle d’un système est la représentation graphique de et de
pour l’ensemble des pulsations
, cette représentation est appelé lieu de transfert et elle se fait dans le plan de BODE.
Enfin, il est impératif de savoir faire le tracé des fonctions de transferts élémentaires :
- Intégrateur :
avec
- Dérivateur :
- Premier ordre :
- Sans nom :
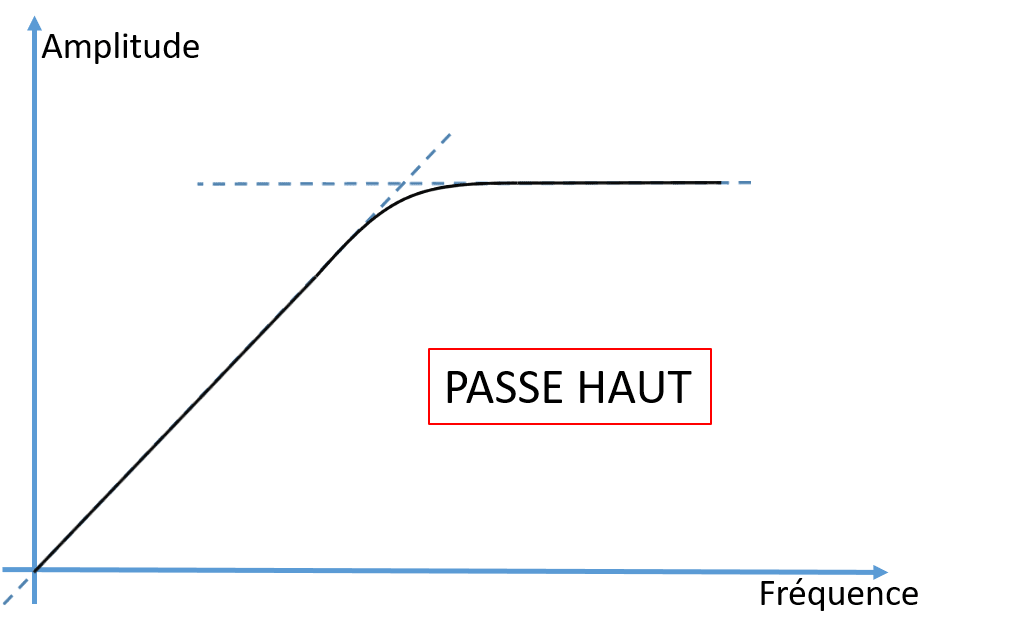
Et de savoir différencier les filtres suivants :






0 commentaires